Construct 3 To 8 Decoder With Truth Table And Logic Gates

Decoder is also a Combinational circuit which transforms given inputs to a maximum number of outputs (maximum outputs equal to 2ⁿ and n are given inputs ).

In other words, a decoder can be defined as a logic circuit that receives binary input and produces output corresponding to that very binary input.

A block diagram of decoder consists of n input lines, one or more enable inputs and 2ⁿmaximum number of output lines.

To construct a decoder, we require to know the number of all possible output lines that totally depends on the given input.

So, if n represents given input lines then possible output lines would be 2ⁿ.
Decoder with three inputs would give 8 outputs (n=2,2³that is 8).

In this article, we’ll be going to design 3 to 8 decoder step by step.

Here are the steps to Construct 3 to 8 Decoder

Step 1. Now we know possible outputs for 3 inputs, so construct 3 to 8 decoder, having 3 input lines, a enable input and 8 output lines.

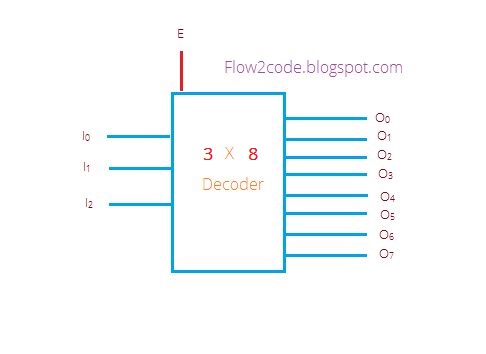
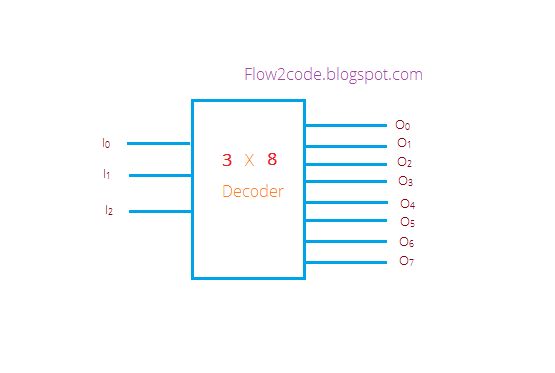
In the below diagram, given input represented as I2, I1 and I0 , all possible outputs named as O_0,O_1,O_2,O₃_,O_4,O_5,O₆_&O₇and a E were represented by Enable input.

With Enable input

Without Enable input

Step 2. Now, it turns to construct the truth table for 3 to 8 decoder. E input can be considered as a control input.

Mean to say, If E equals to 0 then the decoder would be considered as disabled regardless of what inputs are, If E equals to 1 then the decoder would work as per inputs.

Truth table without E input

Inputs			Outputs
I₂	I₁	I₀	O₇	O₆	O₅	O₄	O₃	O₂	O₁	O₀
0	0	0	0	0	0	0	0	0	0	1
0	0	1	0	0	0	0	0	0	1	0
0	1	0	0	0	0	0	0	1	0	0
0	1	1	0	0	0	0	1	0	0	0
1	0	0	0	0	0	1	0	0	0	0
1	0	1	0	0	1	0	0	0	0	0
1	1	0	0	1	0	0	0	0	0	0
1	1	1	1	0	0	0	0	0	0	0

We can represent the following output as:

O₀= I₀‘.I₁‘.I₂‘
O₁= I₀.I₁‘.I₂‘

O₂= I₀‘.I₁.I₂‘
O₃ = I₀.I₁.I₂‘
O₄ = I₀‘.I₁‘.I₂
O₅ = I₀.I₁‘.I₂
O₆ = I₀‘.I₁.I₂
O₇ = I₀.I₁.I₂

Truth table with E input

Inputs				Outputs
E	I₂	I₁	I₀	O₇	O₆	O₅	O₄	O₃	O₂	O₁	O₀
0	-	-	-	0	0	0	0	0	0	0	0
1	0	0	0	0	0	0	0	0	0	0	1
1	0	0	1	0	0	0	0	0	0	1	0
1	0	1	0	0	0	0	0	0	1	0	0
1	0	1	1	0	0	0	0	1	0	0	0
1	1	0	0	0	0	0	1	0	0	0	0
1	1	0	1	0	0	1	0	0	0	0	0
1	1	1	0	0	1	0	0	0	0	0	0
1	1	1	1	1	0	0	0	0	0	0	0

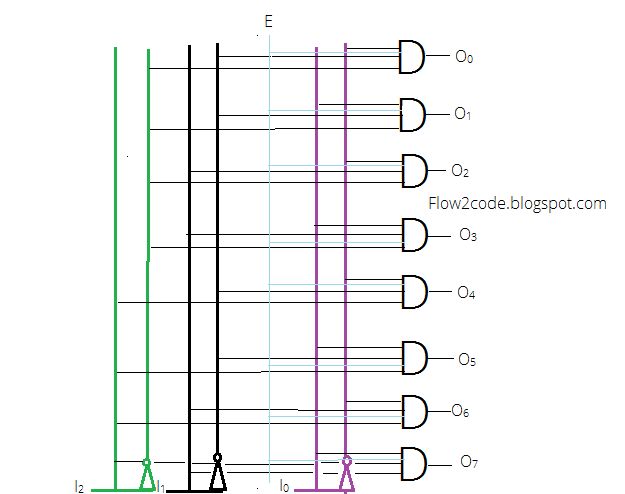
Step 3. With the help of the above expressions derived from the table, the circuit of a 3 to 8 decoder can be implemented.

Decoder Without E

3 2Bto 2B8 2Bdecoder 2Bwithout 2Bflow3code

Explanation:

In the above diagram, there were three input lines with their respective complements using Inverters. Each and every AND gate were holding three inputs from I1, I1 and I0 and producing 8 outputs.

Decoder with E

Explanation:

In above diagram, there were three input lines along with their complements using Inverters. Each and every AND gate were holding four inputs from E, I1, I1 and I0 and producing 8 outputs.

Construct 3 to 8 decoder with truth table and logic gates