A quadratic equation is an equation which must be in the form of ax2+bx+c where a can’t be 0. we use Quadratic formula to find roots and check whether the roots are real or imaginary.
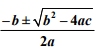
This Quadratic formula is applied only when b2– 4ac >= 0.
such that,
If b2– 4ac > 0 , means the eqn. has more than one real roots
if b2– 4ac = 0 , represent equal or single root
if b2– 4ac <0, represents imaginary root
Lastly, if a is 0, then the equation would not be considered as a quadratic equation.
So, a quadratic equation can have [ Real, Equal, Imaginary, not quadratic ]
We are supposing interval [0,10] where our input values will fall in between this interval and we will create test cases using Boundary Value Analysis accordingly.
Program:
#include<conio.h>
#include<stdio.h>
#include<math.h>
void main()
{
float a,b,c,result;
printf(" ax^2 + bx + c, \n enter the values of a, b and c : = ");
scanf("%f %f %f", &a,&b,&c);
result = (b*b)- (4*a*c);
if(a==0)
printf("not quadratic");
else if(result>0)
{
result= sqrt(result);
printf("Real roots are, %f,%f \n",(-b-result)/(2*a),(-b+result)/(2*a));
}
else if(result==0)
{
result= sqrt(result);
printf("equal root, %f,%f \n",(-b)/(2*a),(-b)/(2*a));
}
else
{
printf("Imaginary root");
}
getch();
}
Testing the Program
Real roots:
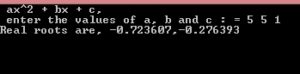
Equal roots:

Not Quadratic
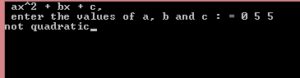
Imaginary :
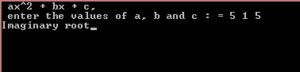
In Boundary Value Analysis, there will be 4N+1 test cases which means 4*3+1 = 13 test cases will be generated
| Test ID | a | b | c | Expected Output | Program Output | Tested Outcome |
|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 5 | Not Quadratic | Not Quadratic | Pass |
| 2 | 1 | 5 | 5 | Real | Real | Pass |
| 3 | 9 | 5 | 5 | Imaginary | Imaginary | Pass |
| 4 | 10 | 5 | 5 | Imaginary | Imaginary | Pass |
| 5 | 5 | 0 | 5 | Imaginary | Imaginary | Pass |
| 6 | 5 | 1 | 5 | Imaginary | Imaginary | Pass |
| 7 | 5 | 9 | 5 | Imaginary | Imaginary | Pass |
| 8 | 5 | 10 | 5 | Equal | Equal | Pass |
| 9 | 5 | 5 | 0 | Real | Real | Pass |
| 10 | 5 | 5 | 1 | Real | Real | Pass |
| 11 | 5 | 5 | 9 | Imaginary | Imaginary | Pass |
| 12 | 5 | 5 | 10 | Imaginary | Imaginary | Pass |
| 13 | 5 | 5 | 5 | Imaginary | Imaginary | Pass |