An equation is said to be a quadratic equation if only if it is in the form of ax2+bx+c where a can’t be 0. We will use the Quadratic formula for calculating the roots to check whether they are imaginary or real.
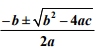
This Quadratic formula is used only when b2– 4ac >= 0. such that, If b2– 4ac > 0 , means the equation has more than one real roots if b2– 4ac = 0 , means equal or single root if b2– 4ac <0, i3mplies imaginary root Lastly, if a is 0, then the equation would not be counted as a quadratic equation.
So, a quadratic equation can have [ Real, Equal, Imaginary, not quadratic ]
Program
Check out “Quadratic Equation” program along with its tested test cases.
Robustness Testing
We are assuming interval [0,10] where our input values will come in between and we will create test cases using Robustness testing accordingly.
In Robustness Testing, it will produce 6N+1 test cases which means, in this case, there will be 6*3+1 = 19 test cases.
| Test ID | a | b | c | Expected Output | Program Output | Tested Outcome |
|---|---|---|---|---|---|---|
| 1 | -1 | 5 | 5 | Invalid Input | Invalid Input | Pass |
| 2 | 0 | 5 | 5 | Not Quadratic | Not Quadratic | Pass |
| 3 | 1 | 5 | 5 | Real | Real | Pass |
| 4 | 9 | 5 | 5 | Imaginary | Imaginary | Pass |
| 5 | 10 | 5 | 5 | Imaginary | Imaginary | Pass |
| 6 | 11 | 5 | 5 | Invalid Input | Invalid Input | Pass |
| 7 | 5 | -1 | 5 | Invalid Input | Invalid Input | Pass |
| 8 | 5 | 0 | 5 | Imaginary | Imaginary | Pass |
| 9 | 5 | 1 | 5 | Imaginary | Imaginary | Pass |
| 10 | 5 | 9 | 5 | Imaginary | Imaginary | Pass |
| 11 | 5 | 10 | 5 | Equal | Equal | Pass |
| 12 | 5 | 11 | 5 | Invalid Input | Invalid Input | Pass |
| 13 | 5 | 5 | -1 | Invalid Input | Invalid Input | Pass |
| 14 | 5 | 5 | 0 | Real | Real | Pass |
| 15 | 5 | 5 | 1 | Real | Real | Pass |
| 16 | 5 | 5 | 9 | Imaginary | Imaginary | Pass |
| 17 | 5 | 5 | 10 | Imaginary | Imaginary | Pass |
| 18 | 5 | 5 | 11 | Invalid Input | Invalid Input | Pass |
| 19 | 5 | 5 | 5 | Imaginary | Imaginary | Pass |
How it is different from Boundary Value Analysis?
We can observe that previously we didn’t check for input values higher than the maximum boundary limit and lesser than the minimum boundary limit. In other words, we haven’t tested our code for Invalid Inputs in Boundary Value Analysis but in Robustness testing, we did make test cases for invalid inputs too and rewrite the code to fulfill this condition.

